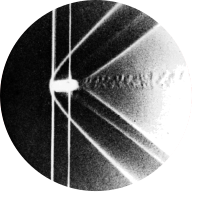
Fig 204. Free convection from a vertical plate

Table of Content

“The plate is uniformly heated in air, producing a steady laminar flow. An interferogram shows lines of constant density which, at nearly constant pressure, are also isotherms. The Grashof number is approximately five million at a distance of 0.1 m from the lower end of the plate, so that the thermal boundary layer is rather thick.” Eckert & Soehngen 1948

Introduction>

Introduction #

In the above experiment, a hot plate is placed inside a room of cooler air, causing heat to transfer from the plate to the air. More specifically, conduction takes place at the interface between the plate and the air, causing the air to heat up, and buoyancy effects then cause the warm air to rise. Buoyancy thus introduces advective heat transport to the problem. Then, what ends up being the dominant heat transport mechanism? And by which physical parameters is this affected? To answer such questions for complex systems (i.e., more complex than a plate in a room), one requires a mathematical model of the flow. Typically, the Boussinesq model is used for simulating temperature-induced buoyant flows. Which assumptions then underlie this model?

In the following, these questions are addressed. We divide this post into two sections: first, we explore the Richardson and Grashof numbers as the dimensionless numbers that capture the relative magnitude of the different heat transfer mechanisms present in the system. Then, we derive the Boussinesq approximation as a simplification of the compressible Navier-Stokes equations. We explore the severity of the underlying approximations by modeling the above system at different temperatures with and without the Boussinesq approximation.

Dimensionless heat transport: Conduction, Convection & Radiation>

Dimensionless heat transport: Conduction, Convection & Radiation #

Three basic principles govern heat transfer: conduction, convection, and radiation. In the experimental photograph above, heat transfer takes place in a fluid (air). Typically, this hints at convection being the largest contributor to the transfer. Nevertheless, conduction remains an important factor as it describes both the transfer from solid to fluid and the mixing of the advecting flow with its surroundings. Radiation can be neglected as its contribution becomes significant only at temperatures above 1000 K [1].

Convective heat transfer can be subdivided into two categories: “forced” and “free” (or “natural”). Simply put, free convection refers to cases where the bulk fluid is initially at rest and buoyancy effects cause the fluid motion, whereas for forced convection, the transporting fluid is driven by external means [2]. However, this distinction becomes blurry when the rising air of a lower segment of the system reaches a significant velocity by the time it interacts with a higher segment of the system. Can we still consider this convection free, or should it be considered forced? The Richardson number provides a handle on estimating which type of convection is at play.

Richardson number (Ri)>

Richardson number (Ri) #

The (forced) convective momentum transport is described by the term $ \boldsymbol{u}\cdot \nabla \boldsymbol{u} $ in the Navier-Stokes equations and thus scales with $ u^2 / L $. The buoyancy term scales with the gravitational acceleration times the volumetric expansion of the fluid. The Richardson number is then defined as their ratio:

$$ \frac{Buoyancy force}{Inertial force} \propto \frac{g \beta \Delta T }{ u^2 / L } = \frac{g \beta \Delta T L }{ u^2 } = Ri $$

Wherein

$u = $ A characteristic velocity of the surrounding fluid $[\frac{m}{s}]$
$L = $ A reference length, e.g., the vertical length of the heated surface $[m]$
$g = $ The gravitational acceleration $[\frac{m}{s^2}]$
$\beta = $ The coefficient of thermal expansion (approximately $\frac{1}{T}$ for an ideal gas, as shown later)
$\Delta T = $ A reference temperature difference, e.g., between the heated surface and the surrounding $[K]$

If the Richardson number is substantially larger than one, buoyancy dominates inertia, indicating a case of free convection. Conversely, if the Richardson number is substantially smaller than one, the system may be considered a case of forced convection. If it is almost equal to one (in order of magnitude), both free and forced convection play an important role [3].

$Ri \gg 1$ : Free convection (ignore forced convection).
$Ri \approx 1$ : Free and forced convection.
$Ri \ll 1$ : Forced convection (ignore free convection).

In earlier posts, we have seen that the Reynolds number is an important dimensionless number that characterizes the nature and stability of a flow. An insightful representation of the Richardson number follows from factoring out the Reynolds number ($Re $). This gives:

$$ Ri = \frac{1}{Re^2}(\frac{g \beta \Delta T L^3}{\nu^2}) = \frac{Gr}{Re^2} $$

With $\nu $ the kinematic viscosity of the fluid $ [\frac{m^2}{s}]$. This form of the equation leads to another dimensionless number: the remainder is called the Grashof number. In the earlier experiment, the Grashof number is stated to equal roughly five million. Additionally, we may assume that the velocity of the fluid remains quite small, and thus that $Re$ is relatively small. It then follows that $Ri $ is substantially larger than 1, indicating a case of free convection.

Grashof number (Gr)>

Grashof number (Gr) #

The Grashof number is often described as the ratio between the buoyancy force and viscous forces acting on the fluid. In that sense, the Grashof number is indicative of the stability of the flow, in much the same way as the Reynolds number. Studies show that for $Gr < 10^8$, the flow typically remains laminar, whereas for $Gr > 10^9$ turbulence occurs [4]. For this interpretation to work, though, the velocity measure in the scaling of the viscous forces (i.e., the $ u $ in $ Viscous force \propto \nu u /L^2 $ ) is replaced by $ u \propto \nu/L $. While this is dimensionally consistent, the implied scaling is rather questionable. Nevertheless, this does motivate the definition of the Grashof number as:

$$ \frac{Buoyancy force}{Viscous forces} \propto \frac{g \beta (T_s - T_{\infty}) }{\nu u / L^2 } \propto \frac{g \beta (T_s - T_{\infty}) L^3 }{\nu^2 } = Gr $$

The Grashof number is reported to be $ Gr \approx 5 \cdot 10^6$ at a distance of 0.1 m from the lower end of the plate. Filling in typical office-room values for $g$, $\beta=1/T_{\infty}$, $T_{\infty}$ and $\nu $ gives an estimated plate temperature of 318.2 K. The value of $ 5 \cdot 10^6$ is also well below the earlier mentioned stability threshold, so that laminar flow can be assumed.

Modeling natural convection>

Modeling natural convection #

Conduction causes the air surrounding the plate to heat up. The increase in temperature leads to thermal expansion of the fluid. Since the mass of a heated fluid parcel stays the same, the volume increase means density decreases. As gravity pulls harder on fluids/objects that are denser, the colder air (with higher density) will experience a higher gravitational pull than the hotter air, causing cold air to drop and hot air to rise. In order of the just described physical processes, we are dealing with the following conservation laws:

Conservation of energy
Conservation of mass
Conservation of momentum

The compressible Navier-Stokes equations>

The compressible Navier-Stokes equations #

As the compressibility of the fluid is the driving factor behind buoyancy, the relevant conservation equations are the compressible Navier-Stokes equations. They read as follows:

Mass (also named continuity): $$ \frac{1}{\rho} \frac{D \rho}{D t} + \nabla \cdot \boldsymbol{u} = 0 $$
Momentum $$ \rho (\frac{\partial\boldsymbol{u}}{\partial t} + (\boldsymbol{u} \cdot \nabla) \boldsymbol{u} ) = - \nabla p + \nabla \cdot \boldsymbol{\tau} + \rho \boldsymbol{g} $$
Energy $$ \frac{\partial}{\partial t} [\rho (e + \frac{1}{2}\boldsymbol{u}\cdot \boldsymbol{u})] + \nabla \cdot [\rho \boldsymbol{u} (e + \frac{1}{2}\boldsymbol{u}\cdot\boldsymbol{u})] = - \nabla \cdot \boldsymbol{q} + \nabla \cdot (\boldsymbol{\tau} \cdot \boldsymbol{u} - p\boldsymbol{u}) + \rho \boldsymbol{u} \cdot \boldsymbol{g} $$

With

$e$ the internal energy per unit mass
$\boldsymbol{q}$ the conductive heat flux vector, for which typically $\boldsymbol{q} = -k\nabla T $ where $k$ is the thermal conductivity
$ \boldsymbol{\tau} $ the viscous stress tensor, for which typically: $\boldsymbol{\tau} = \mu (\nabla \boldsymbol{u} + (\nabla \boldsymbol{u})^T) - \frac{2}{3} \mu (\nabla \cdot \boldsymbol{u}) \boldsymbol{I} $ where $ \mu $ is the fluid dynamic viscosity

As buoyancy is temperature-driven, it is more natural to rewrite the energy equation into an equation for temperature transport.

$$ \rho C_p \frac{\partial T}{\partial t} + \rho C_p \boldsymbol{u} \cdot \nabla T = \nabla \cdot (k \nabla T) + (\frac{\partial p}{\partial t} + \boldsymbol{u} \cdot \nabla p) + \boldsymbol{\tau} : \nabla \boldsymbol{u} $$ with $ T $ the temperature and $C_p$ the heat capacity at constant pressure.

The derivation of the temperature transport equation from the equation conservation energy is quite involved, and can be found by expanding the following box.

Derivation of the temperature transport equation.

Here the equation for conservation of energy will be rewritten to the equation for conservation of enthalpy [5], and subsequently into the temperature transport equation.

Conservation of energy: $$ \frac{\partial}{\partial t} [\rho (e + \frac{1}{2}\boldsymbol{u}\cdot \boldsymbol{u})] + \nabla \cdot [\rho \boldsymbol{u} (e + \frac{1}{2}\boldsymbol{u}\cdot\boldsymbol{u})] = - \nabla \cdot \boldsymbol{q} + \nabla \cdot (\boldsymbol{\tau} \cdot \boldsymbol{u} - p\boldsymbol{u}) + \rho \boldsymbol{u} \cdot \boldsymbol{g} $$

The stress term on the right hand side can be expanded as: $$ \nabla \cdot (\tau \cdot \boldsymbol{u}) = \tau : \nabla \boldsymbol{u} +\boldsymbol{u} \cdot (\nabla \cdot \tau) $$ $$ - \nabla \cdot (p \boldsymbol{u}) = - p \nabla \cdot \boldsymbol{u} - \boldsymbol{u} \cdot \nabla p $$

To reformulate the above conservation of total energy into a conservation equation for the internal energy alone, we subtract the conservation equation of the kinetic energy. This latter equation is obtained from the momentum equation by multiplying it with the velocity $\boldsymbol{u}$. Some algebraic manipulation gives: $$ \frac{\partial}{\partial t} [\rho \frac{1}{2}\boldsymbol{u}\cdot \boldsymbol{u}] + \nabla \cdot (\rho \boldsymbol{u} \frac{1}{2}\boldsymbol{u}\cdot \boldsymbol{u}) = - \boldsymbol{u} \cdot \nabla p +\boldsymbol{u} \cdot (\nabla \cdot \tau) + \rho \boldsymbol{u} \cdot \boldsymbol{f} $$

Performing the subtraction and earlier substitutions then leaves: $$ \frac{\partial}{\partial t} (\rho e) + \nabla \cdot (\rho \boldsymbol{u} e) = - \nabla \cdot q + \tau : \nabla \boldsymbol{u} - p \nabla \cdot \boldsymbol{u} $$

Next, we introduce the enthalpy in place of the internal energy. Their relation is as follows: $$ e = h - \frac{p}{\rho} $$

Substituting the enthalpy relation in the equation for conservation of internal energy (and rearranging it) gives the equation for conservation of enthalpy: $$ \frac{\partial}{\partial t} (\rho h) + \nabla \cdot (\rho \boldsymbol{u} h) = - \nabla \cdot q + \frac{\partial p}{\partial t} + \boldsymbol{u} \cdot \nabla p + \tau : \nabla \boldsymbol{u} $$

The left side of the equation above can be expanded: $$ \frac{\partial}{\partial t} (\rho h) + \nabla \cdot (\rho \boldsymbol{u} h) = h [\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \boldsymbol{u})] + \rho \frac{\partial h}{\partial t} + \rho \boldsymbol{u} \cdot \nabla h = \rho \frac{\partial h}{\partial t} + \rho \boldsymbol{u} \cdot \nabla h $$

Where the second equality is due to mass conservation.

Inserting the equation above into the equation for conservation of enthalpy gives: $$ \rho \frac{\partial h}{\partial t} + \rho \boldsymbol{u} \cdot \nabla h = - \nabla \cdot q + \frac{\partial p}{\partial t} + \boldsymbol{u} \cdot \nabla p + \tau : \nabla \boldsymbol{u} $$

From here, the equation can be rewritten in terms of temperature. The relation between enthalpy, temperature, and pressure is: $$ dh = C_p dT + \frac{1}{\rho} [1 + \frac{T}{\rho} \frac{\partial \rho}{\partial T} ] dp = C_p dT + \frac{1}{\rho} [1 - T \beta] dp $$

Wherein

$\beta = \frac{1}{\rho} \frac{\partial \rho}{\partial T} $ is the coefficient of thermal expansion
$C_p$ is the heat capacity at constant pressure

Since the velocity of the flow is small, $C_p$ can be used in this equation [6].

Substituting the relation above into the equation for conservation of enthalpy gives the equation for conservation of temperature: $$ \rho C_p \frac{\partial T}{\partial t} + \rho C_p \boldsymbol{u} \cdot \nabla T = - \nabla \cdot q + \beta T (\frac{\partial p}{\partial t} + \boldsymbol{u} \cdot \nabla p) + \tau : \nabla \boldsymbol{u} $$

Inserting Fourier’s law: $q = - k \nabla T$ and assuming an ideal gas for which $\beta = \frac{1}{T}$ results in: $$ \rho C_p \frac{\partial T}{\partial t} + \rho C_p \boldsymbol{u} \cdot \nabla T = \nabla \cdot (k \nabla T) + (\frac{\partial p}{\partial t} + \boldsymbol{u} \cdot \nabla p) + \tau : \nabla \boldsymbol{u} $$

Currently, there are four unknowns (velocity, pressure, temperature (energy), and density), but only three equations. One more closure relation is required. For air, we can make use of the ideal gas law as a final closure relation between dependent variables: $$ \rho(p,T) = \frac{p}{R_s T} $$

with $R_s$ the specific gas constant.

The Boussinesq approximation>

The Boussinesq approximation #

For buoyancy-driven flows, small density changes have a significant impact on the behavior of the flow. Consequently, numerical approximation is challenging: small errors in the density field majorly affect the results. To remedy this, one can take a different route. The fluid may be assumed incompressible if the effect of the temperature-induced compressibility is introduced explicitly in the momentum balance equations as a body-force term. This is called the Boussinesq approximation. In the following, we derive the governing equations from the earlier compressible Navier-Stokes equations.

Consider first the equation for conservation of mass. As the density change in the equation for conservation of mass is neglected, i.e., $ \frac{1}{\rho} \frac{D \rho}{D t} = 0$, the velocity field is divergence-free (solenoidal):

$$ \nabla \cdot \boldsymbol{u} = 0 $$

This result can be substituted into the temperature transport equation. Additionally, the velocity gradients can be assumed small, rendering the viscous heating a negligible contribution. Together with a constant density,$ \rho = \rho_0 $, this gives:

$$ \rho_0 C_p \frac{\partial T}{\partial t} + \rho_0 C_p \boldsymbol{u} \cdot \nabla T = \nabla \cdot (k \nabla T) $$

The momentum balance equation requires further elaboration. The Boussinesq approximation follows from writing this momentum balance for the temperature-induced perturbation around a constant-temperature stagnant state. For the constant-temperature stagnant state, the velocity is zero, but the pressure follows the hydrostatic profile. Writing the true pressure field as a perturbation around this hydrostatic state, we get: $ p = - \rho_0 g z + \hat{p} $.

Then, the earlier momentum equation simplifies to: $$ \frac{\partial\boldsymbol{u}}{\partial t} + (\boldsymbol{u} \cdot \nabla) \boldsymbol{u} = - \frac{1}{\rho} \nabla \hat{p} + \frac{\mu}{\rho} \nabla^2 \boldsymbol{u} + \frac{ \rho - \rho_0 }{\rho} \boldsymbol{g} $$

The ideal gas law may then be employed to explicitly relate the temperature change to a density change. A first-order Taylor expansion around $ \rho_0 = \rho(p_0,T_0) $ yields: $$ \rho \approx \rho_0 (1 - \frac{T-T_0}{T_0} ) $$

A detailed derivation on this relation

The ideal gas law is: $$ \rho = \rho (p, T) = \frac{p}{R_{s} T} $$

We define the initial density $ \rho $ as $ \rho_0 $, for which $$ \rho_0 = \rho(p_0, T_0) = \frac{p_0}{R_{s} T_0} $$

The equation for some closely related density $ \rho $ follows from a first-order taylor expansion:

$$ \rho (p+\text{d} p, T+\text{d} T ) = \rho (p_0, T_0) + \frac{\partial \rho}{\partial p}\Big|_{{p_0,T_0}} \text{d}p + \frac{\partial \rho}{\partial T} \Big|_{{p_0,T_0}} \text{d} T $$

$$ = \rho_0 + \frac{1}{R_{s} T_0} \text{d} p - \frac{p_0}{R_{s} T_0^2} \text{d} T $$

$$ = \rho_0 + \frac{\rho_0}{p_0} \text{d} p - \frac{\rho_0}{T_0} \text{d} T $$

$$ = \rho_0 (1 + \frac{\text{d} p}{p_0} - \frac{\text{d} T}{T_0}) $$

We now make the assumption that: $$ \frac{\text{d} p}{p_0} = \frac{p-p_0}{p_0} \ll \frac{T-T_0}{T_0} = \frac{\text{d} T}{T_0} $$

Such that we may simplify the approximation of the density $\rho$ as: $$ \rho \approx \rho_0 (1 - \frac{T-T_0}{T_0} ) $$

The above assumption is indeed valid for the considered experiment because:

the atmospheric pressure has an order of magnitude of $10^5$
the change in pressure has an order of magnitude of $10^{-3}$ (confirmed in Ansys)
the change in temperature has an order of magnitude of 10$10$ (between $10^{-1}$ and $10^2$)
the room temperature has an order of magnitude of $10^2$
this gives for the assumption: $ \frac{10^{-3}}{10^5} = 10^{-8} \ll \frac{10}{10^2} = 10^{-1}$

Substitution of this approximation into the momentum balance equation gives: $$ \frac{\partial\boldsymbol{u}}{\partial t} + (\boldsymbol{u} \cdot \nabla) \boldsymbol{u} = - \frac{1}{ \rho_0 (1 - \frac{T-T_0}{T_0} )} \nabla \hat{p} + \frac{\mu}{ \rho_0 (1 - \frac{T-T_0}{T_0} )} \nabla^2 \boldsymbol{u} - \frac{ \frac{T-T_0}{T_0} }{ 1 - \frac{T-T_0}{T_0} } \boldsymbol{g} $$

Recall that the fields $ \boldsymbol{u} $ and $\hat{p} $ are interpreted as temperature-induced perturbations. As such, they are assumed to scale with the temperature perturbation, i.e., $ T-T_0$. Considering only leading-order terms, those of order $ T-T_0 $, the above simplifies to: $$ \frac{\partial\boldsymbol{u}}{\partial t} + (\boldsymbol{u} \cdot \nabla) \boldsymbol{u} = - \frac{1}{ \rho_0 } \nabla \hat{p} + \nu_0 \nabla^2 \boldsymbol{u} - \frac{T-T_0}{T_0} \boldsymbol{g} $$

In summary, the equations for describing convective heat transport with the Boussinesq approximation are:

Conservation of mass: $$ \nabla \cdot \boldsymbol{u} = 0 $$
Conservation of momentum $$ \frac{\partial\boldsymbol{u}}{\partial t} + (\boldsymbol{u} \cdot \nabla) \boldsymbol{u} = - \frac{1}{ \rho_0 } \nabla \hat{p} + \nu_0 \nabla^2 \boldsymbol{u} - \frac{T-T_0}{T_0} \boldsymbol{g} $$
Temperature transport (following from conservation of energy). $$ \rho_0 C_p \frac{\partial T}{\partial t} + \rho_0 C_p \boldsymbol{u} \cdot \nabla T = \nabla \cdot (k \nabla T) $$

The incompressible Boussinesq approximation significantly simplifies the heat transport equations compared to the compressible approximation. This makes it easier to use the equations in a simulation [7]. Since this approximation also represents reality reasonably well at low density changes, it is commonly used in heat transport studies like the present one. Another reason for using this incompressible Boussinesq approximation is that for the compressible approximation, convergence of the simulations is more important to obtain accurate results since a small deviation has a big impact.

Simulation results>

Simulation results #

Comparison between compressible Navier-Stokes and Boussinesq approximation>

Comparison between compressible Navier-Stokes and Boussinesq approximation #

The incompressibility assumption simplifies all three conservation equations. For these simplifications to be appropriate, the density changes must be small, and therefore so must the temperature changes. The Boussinesq approximation itself also assumes small temperature variations. So, it is expected that at small temperature changes, the incompressible Boussinesq approximation gives a good representation of reality, while with larger temperature changes, results are less accurate. Now that the (theoretical) differences between both approximations are known, it is interesting to see how these manifest themselves in simulations. As a study case, we use the above experiment that Eckert and Soehngen executed in the late 1940s.

In the experiment, a Zehnder-Mach interferometer was used to photograph the isotherms. The experiment took place inside their laboratory, so general room conditions apply. The domain is modeled to be 2D, since the depth of the initial copper plate is large (around 609.6 mm) compared to the height and width (respectively 127 mm and 3.97 mm). In the experiment, the photograph was made shortly after the copper plate was placed inside the room (the researchers tried to do it immediately). To mimic this, we use a transient model to simulate the first few seconds of heat transport. The 2D model of the plate is put inside a much larger box so that the domain restrictions do not influence the solution field near the plate. The meshes used for the simulation are illustrated below.

The sliders below then show the two approximations using three different initial temperature differences between the plate and the fluid (respectively: 0.3 K, 30.3 K, and 336.4 K, corresponding to Grashof numbers of $0.1\cdot 10^6$, $9\cdot 10^6$ and $100\cdot 10^6$, respectively). The gray-scale visualization is obtained by plotting the temperature field and then setting the bounds of a colorbar to the room temperature and plate temperature, and by choosing as many black-to-white intervals as there are bands in the experimental photograph.

“At Gr=100.000; Compressible vs Incompressible Boussinesq approximation (in simulation at t=3 seconds); the initial temperature difference is 0.3 K”

“At Gr=9.000.000; Compressible vs Incompressible Boussinesq approximation (in simulation at t=3 seconds); the initial temperature difference is 30.3 K”

“At Gr=100.000.000; Compressible vs Incompressible Boussinesq approximation (in simulation at t=3 seconds); the initial temperature difference is 336.4 K”

At a small temperature difference, one can see that both approximations give a similar result. When the temperature difference increases, the results of the two approximations are less aligned. At a d$T$ (temperature change) of 30.3 K, the difference is relatively small, while at a d$T$ of 336.4 K, one can see the differences well. At a d$T$ of 0.3 K, the theory expected the incompressible Boussinesq approximation to be more reliable. The simulation results of both approximations show almost similar results, which confirms the theory and illustrates that the incompressible Boussinesq approximation is useful. When d$T$ increases, the differences between the results of both approximations increase as well. This is also expected since the incompressible Boussinesq approximation becomes less reliable, and therefore the compressible approximation should be used at larger d$T$.

Comparison between simulation and experiment>

Comparison between simulation and experiment #

Finally, we compare the simulation results for the Boussinesq approximation to the experimental photograph. The researchers estimate a plate temperature of 318.2 K at the moment the picture was made (as derived from their stated value for the Grashof number: $Gr = 5 \cdot 10^6$). However, a best simulation match is found for a temperature of 323.3 K (corresponding to $Gr = 9 \cdot 10^6$). We consider this 5-degree temperature within uncertainty tolerances, as the researchers do not mention the plate temperature explicitly, nor do they state the equation and values they used to determine the Grashof number. For this plate temperature, we obtain:

The simulation and experiment match very well. The main mismatch is the isotherm furthest away from the plate. In the experiment, this is not quite straight, probably being the result of some external air currents (forced convection).

Summary>

Summary #

When a hot plate is placed inside a room of air, the air directly surrounding the plate heats up due to conduction. As the air gets hotter, the volume increases, which means the density decreases. Air with a higher density is pulled onto harder by gravity so that it pushes the air with the lower density (the hot air) upwards. This net upwards force is called the buoyancy force. The moving air adds convection to the heat transport problem.

Whether the convection can be considered “free” (the bulk fluid is not moving) or “forced” (the bulk fluid moving due to an external source) is determined by the Richardson Number ($Ri = \frac{Gr}{Re^2}$). In this study, the Richardson number is substantially larger than 1, so that free convection is at play. This means the Grashof number ($Gr = g \beta (T_s - T_{\infty}) L^3 / \nu^2 $) is the dimensionless number that predominantly describes the behavior of the flow.

To simulate the buoyancy-induced convective flow, the physics is described by three conservation laws: those for mass, momentum, and energy (temperature). Jointly, these are the compressible Navier-Stokes equations. Additionally, the Ideal Gas Law is used to relate pressure, temperature, and density. To simplify the equations, one may consider using instead the equations for incompressible flow while adding the Boussinesq approximation for a buoyancy force in the equation for conservation of momentum. While this approximation considerably simplifies the numerical approximation procedure, it is only valid for small temperature changes. The earlier example simulations confirm this difference between the two approximations.

Sources>